Positions Through Iterating

I took as my ‘iteration zero’ for this project a Lindenmayer system visualisation I’d coded in Methods of Iterating, for which I had used p5.js:

This was based upon the rules for drawing Fig 1.24.e with Turtle graphics from page 37 of ‘The Algorithmic Beauty of Plants’ (Prusinkiewicz and Lindenmayer, 2004):

var angle;
var axiom = "X";
var sentence = axiom;
var len = 200;

var rules = [];
rules[0] = {
  a: "X",
  b: "F[+X][-X]FX",
};

rules[1] = {
  a: "F",
  b: "FF",
};

function generate() {
  len *= 0.5;
  var nextSentence = "";
  for (var i = 0; i < sentence.length; i++) {
    var current = sentence.charAt(i);
    var found = false;
    for (var j = 0; j < rules.length; j++) {
      if (current == rules[j].a) {
        found = true;
        nextSentence += rules[j].b;
        break;
      }
    }
    if (!found) {
      nextSentence += current;
    }
  }
  sentence = nextSentence;
  createP(sentence);
  turtle();
}

function turtle() {
  background(51);
  resetMatrix();
  translate(width / 2, height);
  stroke(255, 100);
  for (var i = 0; i < sentence.length; i++) {
    var current = sentence.charAt(i);

    if (current == "F") {
      line(0, 0, 0, -len);
      translate(0, -len);
    } else if (current == "+") {
      rotate(angle);
    } else if (current == "-") {
      rotate(-angle);
    } else if (current == "[") {
      push();
    } else if (current == "]") {
      pop();
    }
  }
}

function setup() {
  createCanvas(500, 500);
  angle = radians(25.7);
  background(51);
  createP(axiom);
  turtle();
  var button = createButton("generate");
  button.mousePressed(generate);
}

I was interested in further exploring ideas pertaining to the continuous versus the discrete, the capacity for mathematical rules to be expressed in different visual “style[s]” (Ording, 2019), and the parallel of organic forms grown from genetic code with graphics on a screen being “grown” from JavaScript.

I kept most of the code the same, but iterated through angle variations for my 100-page publication e.g. 15°, 30°, 45°, 90°, etc., generating iterations of each angle until the code crashed due to a potential infinite loop.

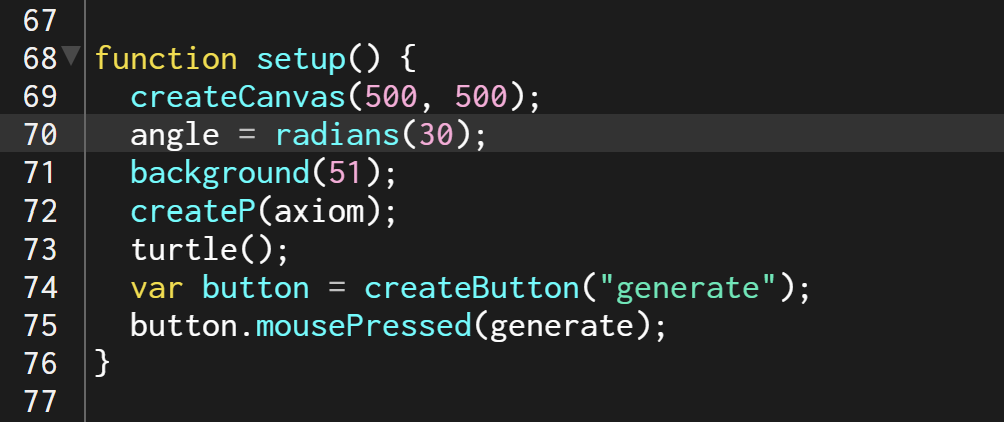
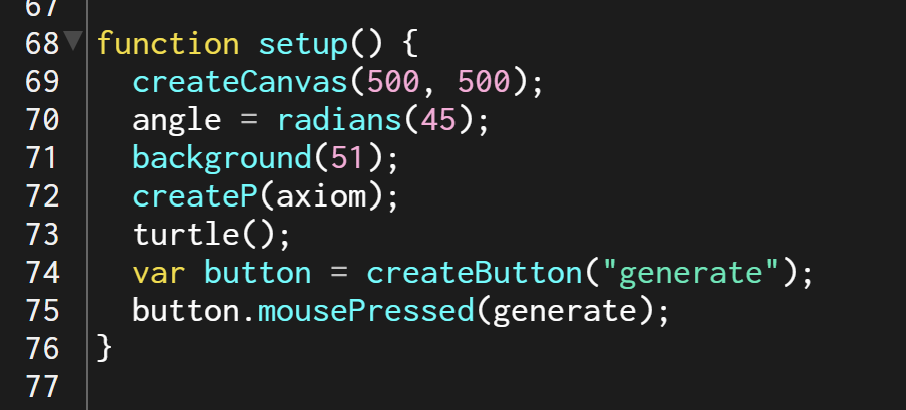
angle = radians(15);

angle = radians(30);

angle = radians(45);

angle = radians(60);

angle = radians(75);

angle = radians(90);

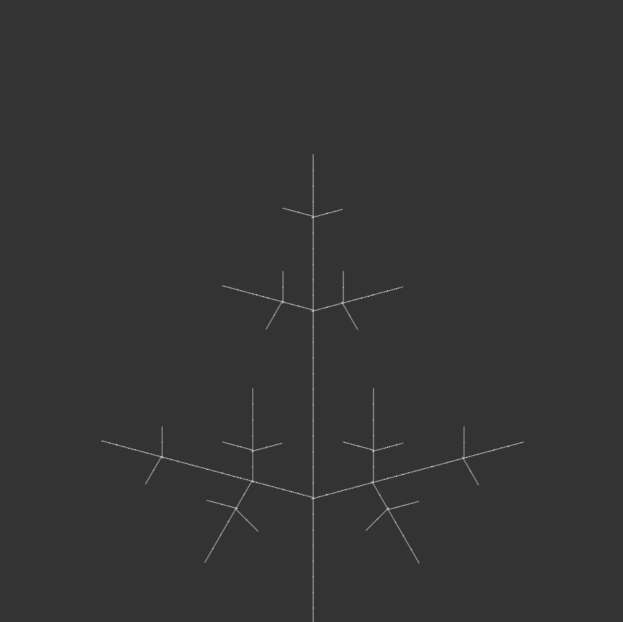
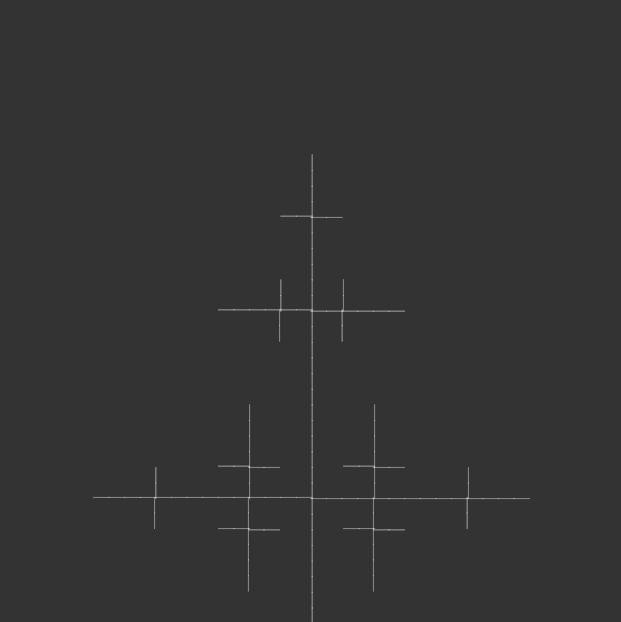
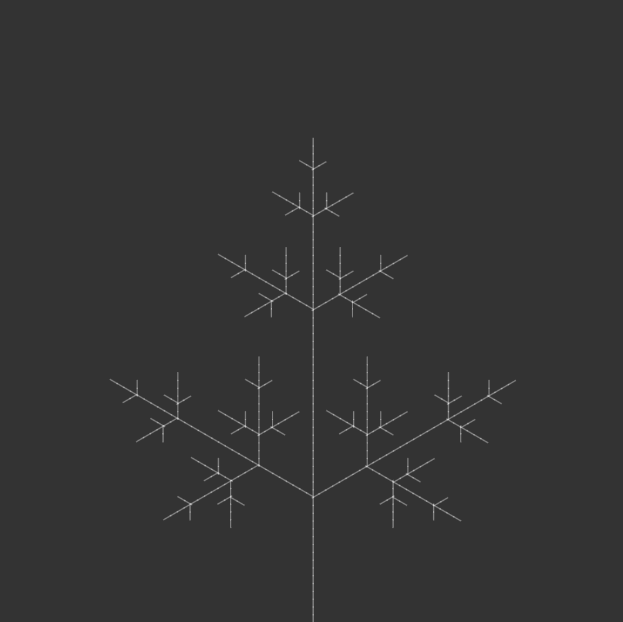
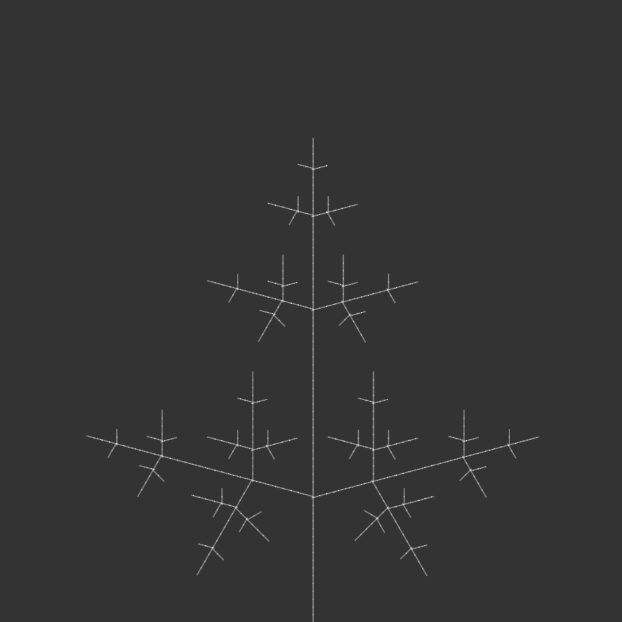
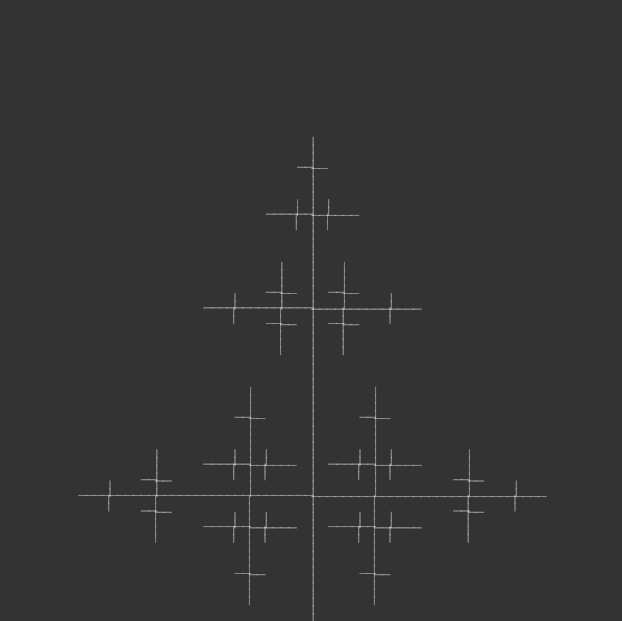
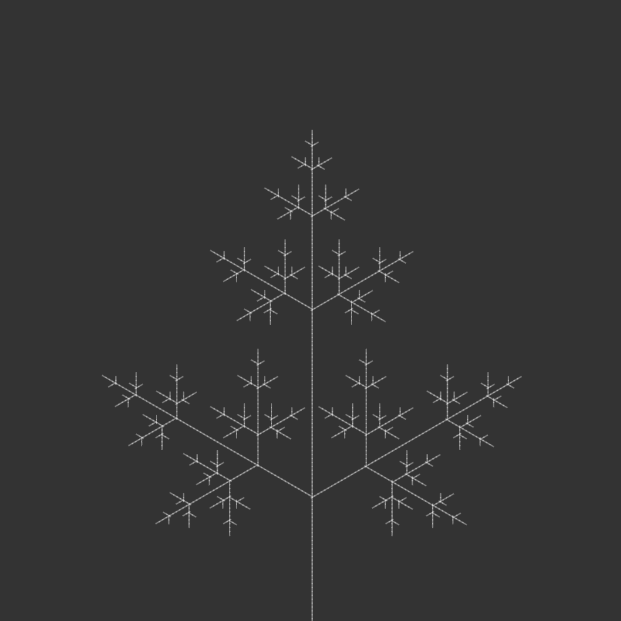
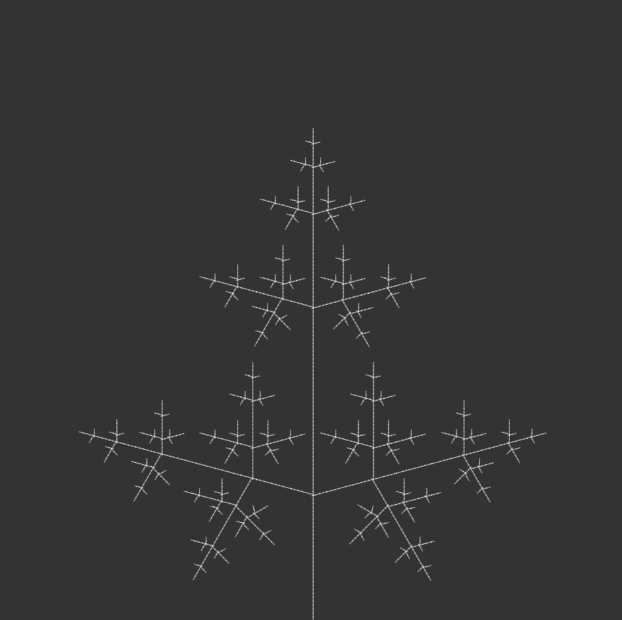
angle = radians(105);

angle = radians(120);

angle = radians(135);

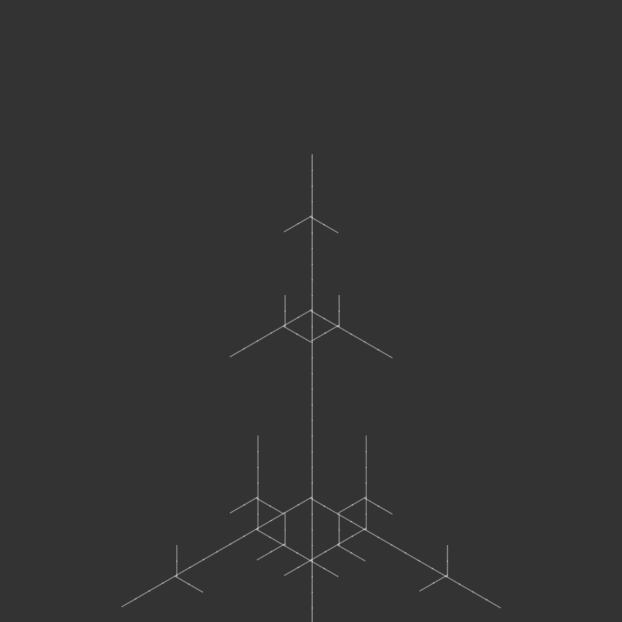
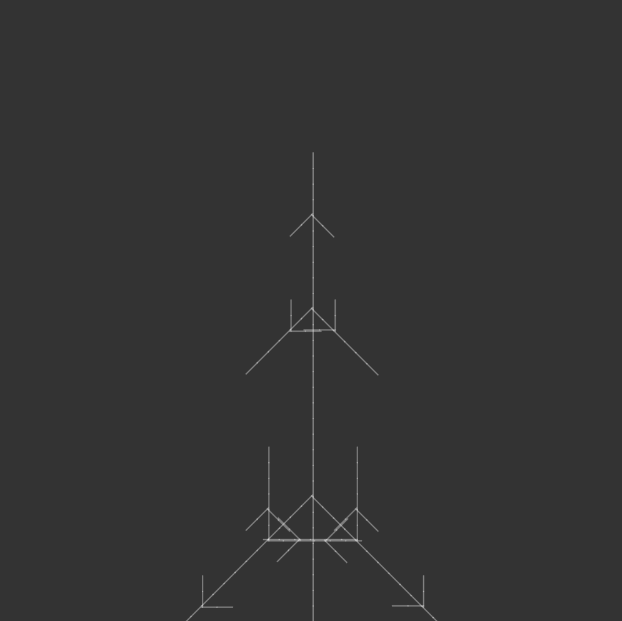
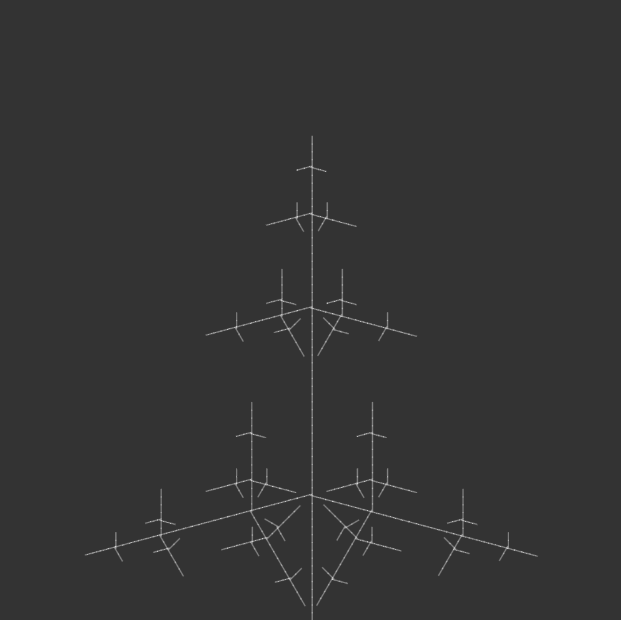
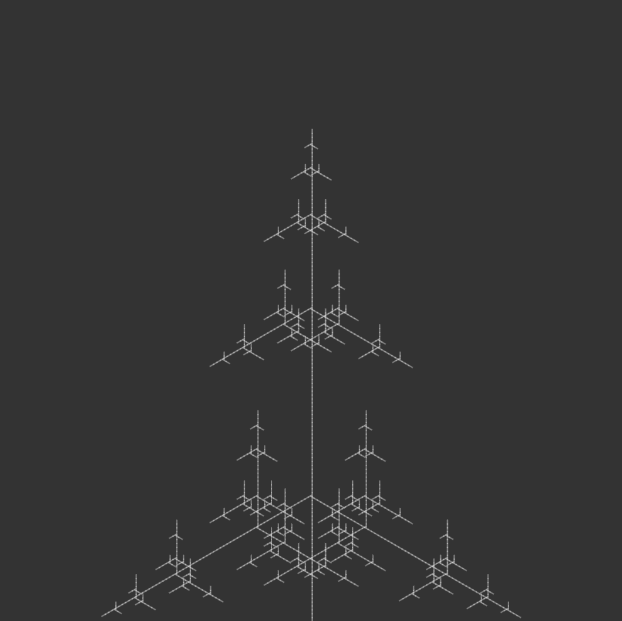
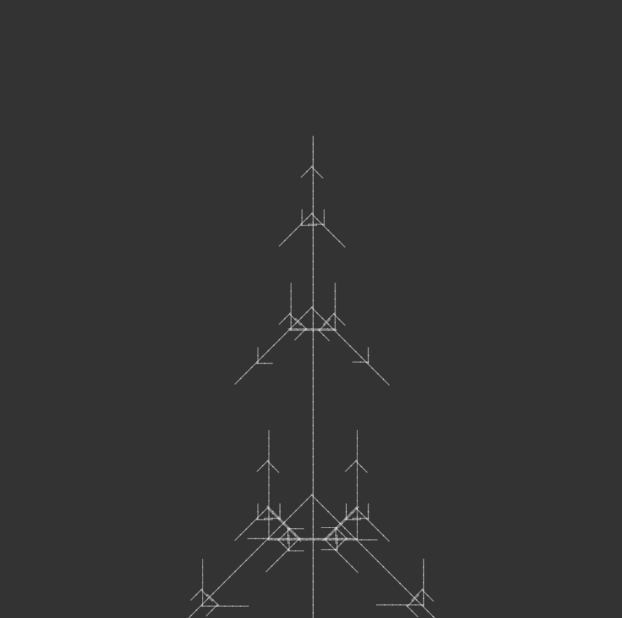
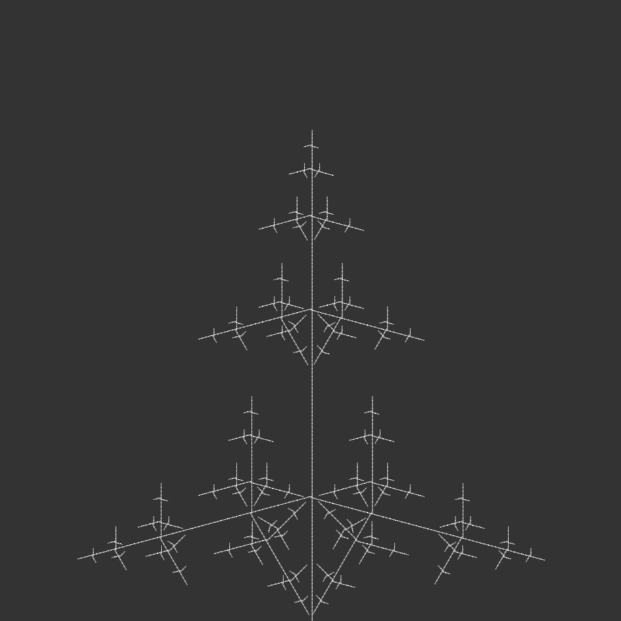
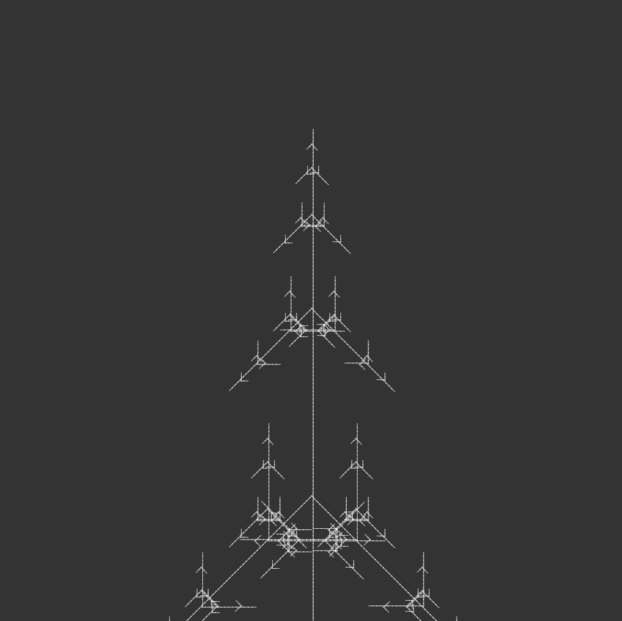
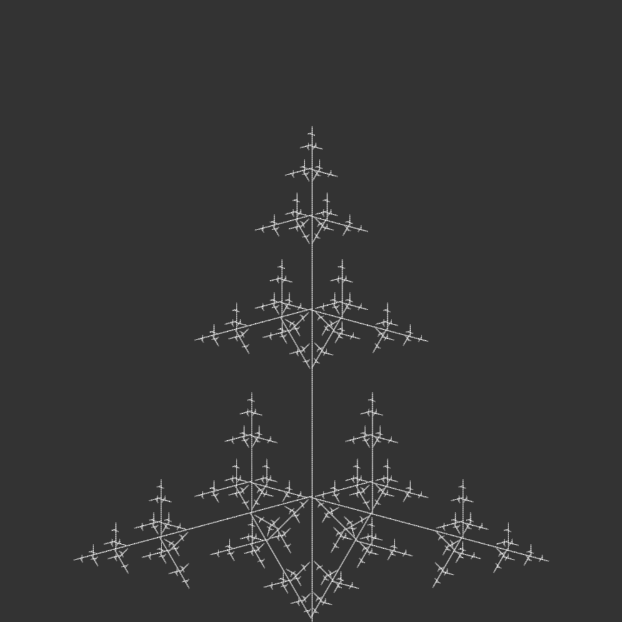
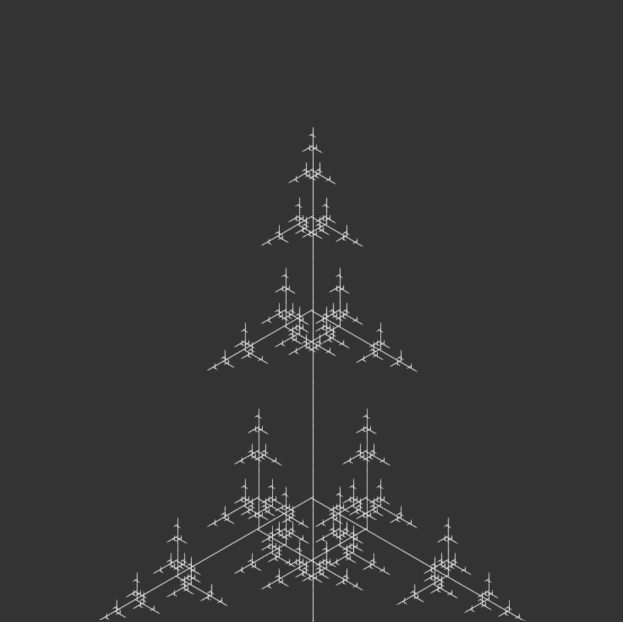
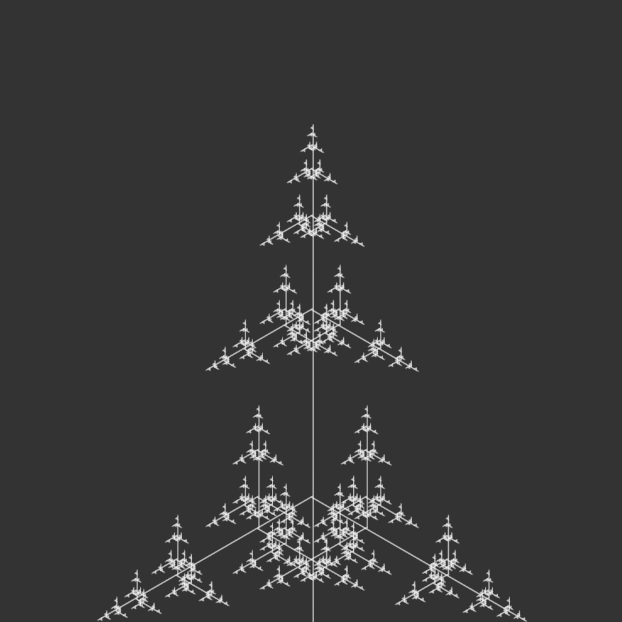
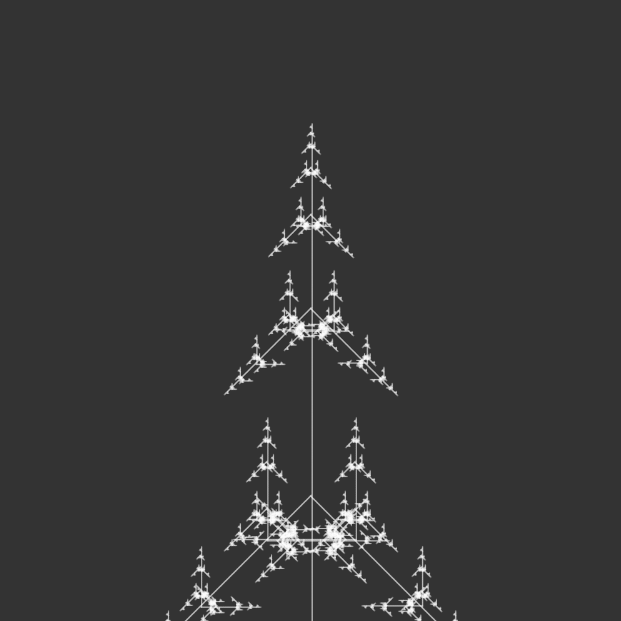
angle = radians(150);

angle = radians(165);

angle = radians(180);

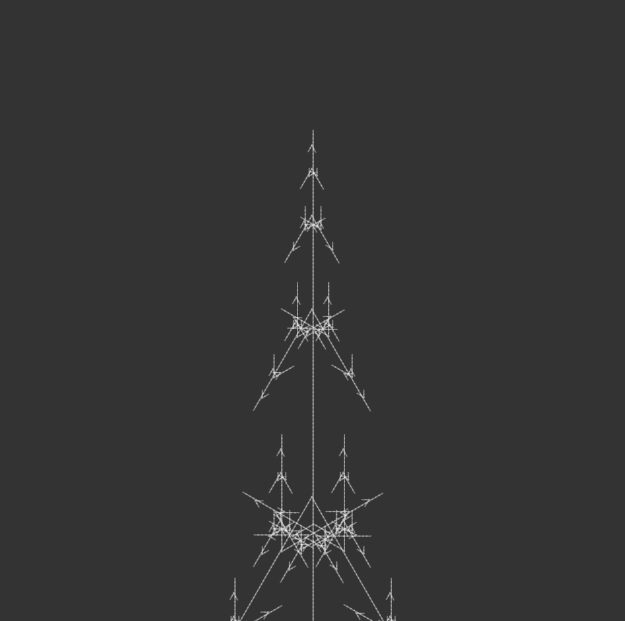
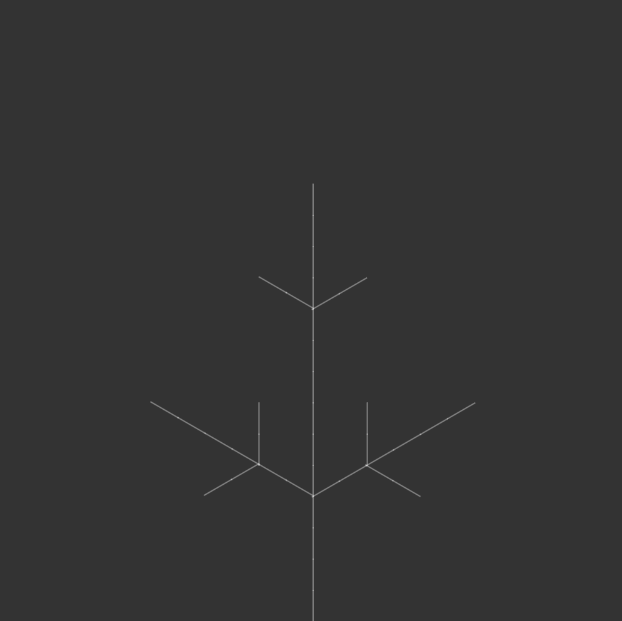
I bound the publication with metal rings to simulate an infinite loop, as a continuous flipbook, and ordered them in opposite directions: the first in ascending iterations, the second in descending iterations, the third in ascending, and so on. This was to reinforce the feeling of a cycle, with the plant growing and wilting, but also changing form. Sometimes it resembled a real plant, sometimes it resembled other natural structures, like a snowflake. Or sometimes it looked like nothing natural at all, but an assemblage of symmetrical lines.

Snippets of the prototype:

Which, when looped together, tell this story:

I assembled the images to print using Microsoft Word, and it was interesting to see the alternative text descriptions which were generated (I had considered alt-text descriptions in Methods of Translating: Charbonnel et Walker and ‘how machines read’ in the XY studio, Technology 2). This is how my machine read the story:

Following an excerpt from the book, ‘The Language of Trees’, I considered further the filling of trees in a forest space and considered what that might look like with p5.js.

Of course, in real life, trees exhibit ‘crown shyness’ and a kind of spatial respect for one another in the course of competing for light and resources. These coded experiments, though they follow their coded rules, do not follow “natural” rules of plants in space: some of the generated trees have unrealistic branching patterns and overlap in unnatural ways. But according to The Algorithmic Beauty of Plants, “a departure from realism may offer a fresh view of known structures”.