I had a Teams meeting with José García Oliva, in which I showed him my video essay and my blog. He asked me what my aim for the project was. I said I wasn’t yet sure.
We talked about Ogham (‘the Celtic Tree alphabet’) and my idea to encrypt information with a new Lindenmayer branching alphabet. He mentioned Latin being an abstraction and recommended looking at cuneiform. It can be interesting to see how light interacts with scripts which are inscribed, rather than written. I hadn’t thought before of how plants need light to grow but we also need light to read visually. The genetic information in a plant needs light to reach its full potential, and the visual information it forms needs light to reach our eyes.
‘What do you want people to get out of it?’, José posed. Maybe it could be a kind of universal communication? Like an Isotype (the picture language). Having looked up Isotype, its main aim was ‘visual education’ or that of a ‘helping language’, but to embed information in a tree cipher is secret rather than explanatory.
If I were to develop a Lindenmayer alphabet using my existing structure, it might be possible to compound words in a similar way to Aengus Woods’ illustration, wherein each letter is represented by branching of a specific type, and letters in a word are compounded upon a linking stem, but a space separates them to a new branch. José suggested going to a park and applying this language – what do the trees say? Is there a particular tree I am looking at? One could decode a location. Upon reflection, my current system wouldn’t be very effective as real-life branches usually all reach upwards, and my system which includes horizontal/downward-facing branches, so some letters would never occur. Also, the Lindenmayer alphabet is two-dimensional, without consideration of multiple branches reaching out radially in any direction.
In regard to the mathematical dimension of my project, José suggested looking at the Golden Ratio, which is perhaps the best-known connection between mathematics and design. I wonder what it would mean to apply the golden ratio to my Lindenmayer systems – would they appear more beautiful? We discussed mathematics being a universal language. I wonder what that means in terms of translation – is there a sense in which mathematics is an interface between all peoples, but also between us and the real world? Reminds me once again of Wigner’s ‘unreasonable effectiveness of mathematics’.
The linkage of language (mathematical language, as well as the idea of encrypting English language into Lindenmayer branches) and my textile interpretations also led to discussions about the languages of weavers from indigenous people groups in Latin America. They are mainly women (Smith, 2018) and wear hand-woven embroidered huipils. The languages of their forefathers are dying out, but were sometimes written in glyphs rather than how they are represented in the Latin alphabet today. Maybe there is another tree of thought that could be grown here, in thinking about translation and hiddenness of meaning.
I have contacted others who haven’t (yet) replied.
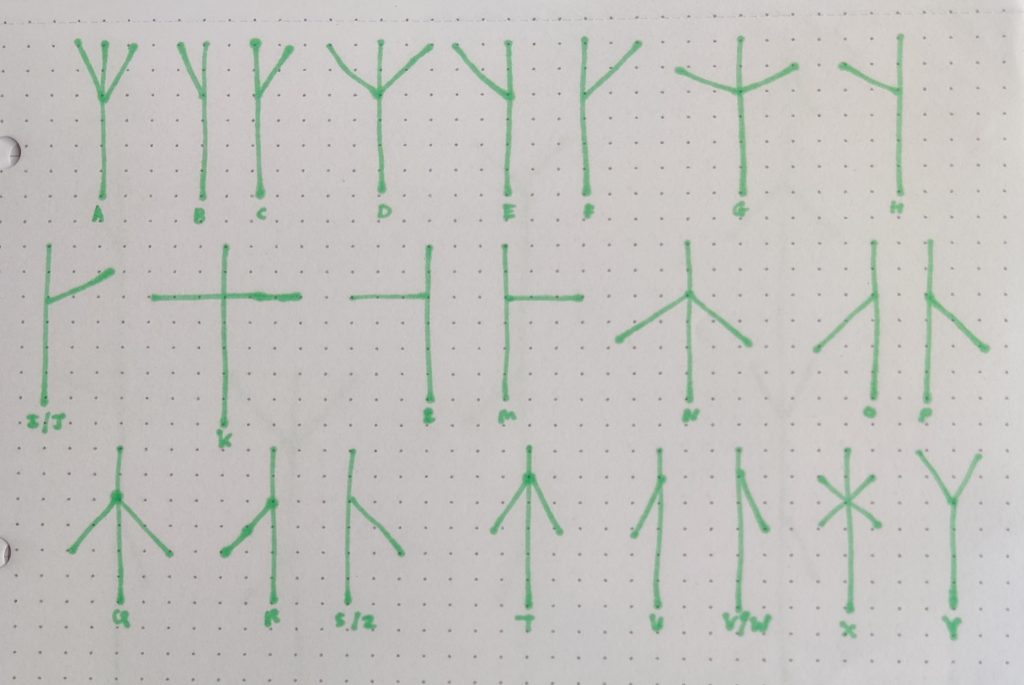
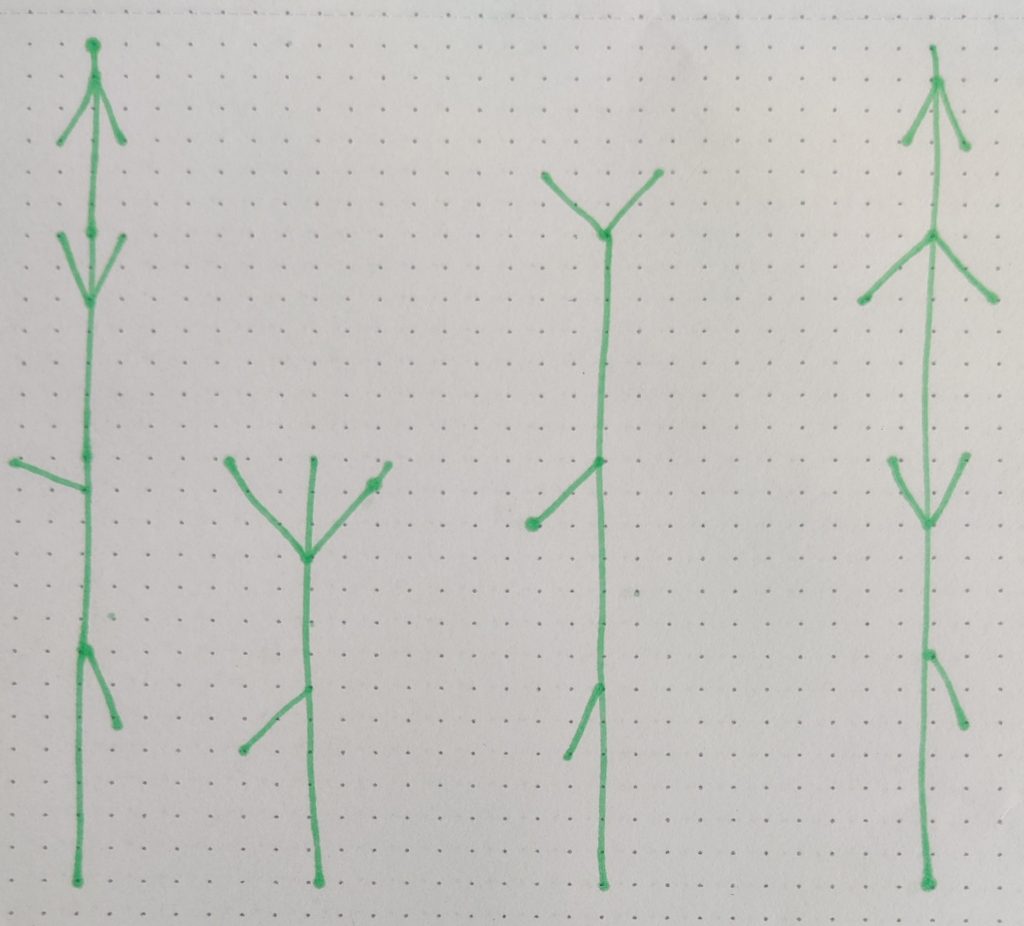
- García Oliva, J. (2024) Microsoft Teams conversation with Kathryn Jones, 7 June.
- ‘Isotype (picture language)’ (2023) Wikipedia. Available at: https://en.wikipedia.org/wiki/Isotype_(picture_language)#cite_note-3 (Accessed: 18 September 2024).
- Smith, L. (2018) Ancient tongues: The languages of our weavers. Available at: https://tramatextiles.org/blogs/trama-blog/ancient-tongues-the-languages-of-our-weavers
- Wigner, E. (1960) ‘The Unreasonable Effectiveness of Mathematics in the Natural Sciences’, Communication in Pure and Applied Mathematics.
- Woods, A. (2023) ‘Of Trees in Paint; in Teeth; in Wood; in Sheet-Iron; in Stone; in Mountains; in Stars’ in K. Holten (ed.) The Language of Trees. Portland, Oregon: Tin House, p225-231.